How To Draw A Topographic Profile

3.half dozen: Cartoon Contour Lines and Topographic Profiles

Concluding updated
Save every bit PDF

Page ID: 5473

Professors (Paleontology & Geology) at University of West Georgia
Source: GALILEO Open up Learning Materials

Overview

Constructing a topographic map by drawing in contours can be hands done if a person remembers the post-obit rules regarding contour lines:

Contour lines stand for lines connecting points of equal elevation above body of water level
Contour lines never cross, dissever, or die off
Contour intervals must be obeyed, therefore the contour line elevations can only exist multiples of the contour interval
Contour lines make a "v" pattern as they cross streams and rivers, and the "v" e'er points towards the upstream direction.

As you depict a contour line on a map yous will notice that the elevations on i side of your line volition exist lower elevations, and elevations on the other side of your line will be college elevations. Once your contour lines are drawn, yous will observe that yous had to draw some lines closer together in some areas and wider apart in other areas and that yous may accept even enclosed an area by drawing a contour line in a circular pattern. These round patterns indicate hilltops, like in the diagram below (Effigy iii.6). To illustrate what these hills await like in contour (or, how they would look if y'all saw them while continuing on the footing and looking at them from a distance), you can describe what is known as a topographic profile. Essentially a topographic profile is a side prototype of a topographic map, only the image is only a representation of the area shown on the line on the topographic map (line A-B on Figure 3.6).

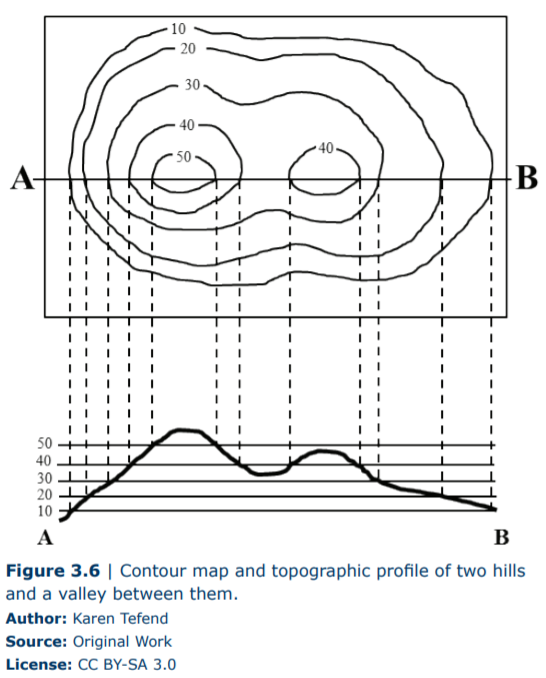
To construct a profile, you need graph paper, a ruler, and a pencil. You want to have the y-centrality of the graph newspaper represent the elevations of the contour lines that intersect your drawn line (line A-B in this instance). Past using a ruler, you lot tin transfer these pinnacle points from your topographic map directly downwards onto your graph paper such as shown in Effigy 3.6. Be sure to merely plot those elevations that are at the intersection of the contour line with line A-B. Once your points are plotted on the graph paper, you simply connect the dots. As a rule, hilltops will be slightly rounded to show a slight increment in elevation to represent the crest of the hill, just exist careful not to describe the hilltop too loftier on your graph paper. For example, the first hill on the left has a top contour line of 50ft. Because there isn't a 60ft contour line on this hilltop, we know that the hill'southward highest point (the crest) is some superlative between 50 and 60ft.

When connecting the points on your graph paper in the surface area betwixt the two hills in Effigy three.vi, y'all again want to round out the expanse to correspond the base of your valley between the hills, but be careful not to brand the valley floor too deep, as according to the topographic map the elevation is below 40ft, merely non as low equally 30ft.

If you examine the graph showing the topographic profile in Figure 3.half dozen, can you imagine what would happen to your profile if we inverse the spacing for elevations on the y-centrality? When the vertical dimension of your graph is different from the horizontal dimension on your map, you may end upwardly with a graph that shows a vertical exaggeration and the features of the Globe represented by your topographic profile may be deformed such equally in Figure 3.7.

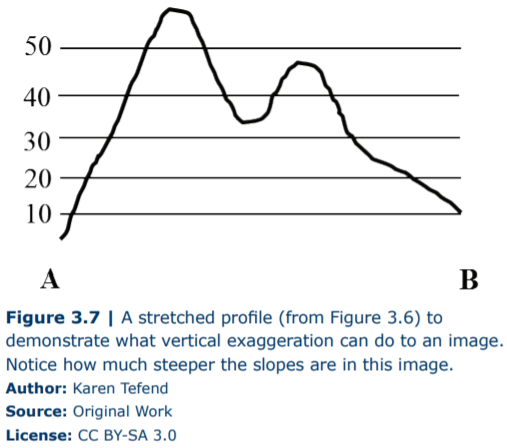
Sometimes vertical exaggeration is desired simply, in some cases, y'all may not desire it. To avoid having your profile distorted so that it accurately conveys what the surface of the Earth actually looks like in profile, you volition desire both the vertical and horizontal scales to match. For instance, if your map calibration is 1 inch = fifty ft, then one inch on your graph's y-axis should simply represent 50ft of elevation. If the topographic map in Figure 3.6 has a fractional scale of 1:12,000 then one inch is equal to 12,000 inches or 1000ft; this 1inch = 1000ft equivalency is for the horizontal scale. When nosotros hold a ruler to the y-axis of the topographic profile in Figure 3.6, we meet that 0.five inches = 50ft, which means 1 inch = 100ft on the vertical scale. To calculate the vertical exaggeration in the topographic profile shown in Figure 3.6 we divide the horizontal scale past the vertical scale: (\(\frac{\frac{one thousand\;ft}{ane\;inch})}{(\frac{100\;ft}{inch}}) = 10\). Therefore the topographic profile in Figure 3.6 represents a profile of the map surface (along the A-B line) that has been vertically exaggerated past x times (10X).

Answers to Do Lab Exercises, Parts A and B

76°xv'00" W longitude
43°00'00" N breadth
2000 ft
ane ft = 24,000 ft, and 24,000 ft 10 (\(\frac{1\;km}{3280\;ft}\)) = seven.32 km
S

Source: https://geo.libretexts.org/Learning_Objects/Laboratory/Book%3A_Laboratory_Manual_For_Introductory_Geology_(Deline_Harris_and_Tefend)/03%3A_Topographic_Maps/3.6%3A_Drawing_Contour_Lines_and_Topographic_Profiles

Posted by: stevensspattent.blogspot.com